
Percentage – Introduction, Uses and Formula
Percentage is a mathematical concept that is used to explain a portion or fraction of a whole as a number out of 100. The term “percent” means “per hundred.” It is denoted by the symbol “%”. Percentages are widely used in various fields to represent relative values, make comparisons, and understand proportions.
Formula for Calculating Percentage
To calculate a percentage, you can use the following formula:
Percentage = (Part / Whole) × 100
In this formula, “Part” refers to the specific value or quantity you are interested in, and “Whole” represents the total value or quantity. By dividing the part by the whole and then multiplying the result by 100, you obtain the percentage value.
Uses of Percentage
Proportions and Ratios: Percentages are used to represent proportions and ratios in a convenient and standardized manner. For example, if a class has 30 boys out of a total of 50 students, you can express the proportion of boys as 60% (30/50 × 100).
Comparisons: Percentages allow for easy comparisons between different quantities or values. They help in understanding the relative significance or change between two or more items. For instance, if a stock price increases from $50 to $60, you can say it has risen by 20% (10/50 × 100).
Discounts and Sales
Percentages are commonly used to calculate discounts during sales or promotional offers. If an item is discounted by 30%, you can easily determine the reduced price by subtracting 30% of the original price from it.
Interest Rates:
Percentages are used to express interest rates in financial transactions. For example, a bank might offer a 5% annual interest rate on a savings account, indicating that you will earn 5% of your initial deposit as interest each year.
Statistics and Data Analysis
Percentages are crucial in statistics and data analysis to interpret and present data effectively. They help in understanding the distribution of values, frequencies, and proportions within a dataset.
Growth and Change
Percentages are useful for measuring growth rates, changes, or improvements over time. They provide a standardized way to express the increase or decrease in a quantity. For example, if a company’s revenue grows from $1 million to $1.5 million, you can say it has experienced a 50% growth in revenue.
What is Percentage?
The word “percent” literally means “per hundred.” It is denoted by the symbol “%”. Percentages are commonly used to represent parts of a whole or to compare quantities. They allow us to easily understand and communicate relative values. For example, if you have a pizza and you eat three out of eight slices, you can say that you have consumed 37.5% of the pizza.
Percentages are used in various real-life situations, such as calculating discounts, expressing interest rates, understanding statistical data, analyzing trends, and many more. They provide a standardized way to represent proportions and facilitate comparisons across different quantities.
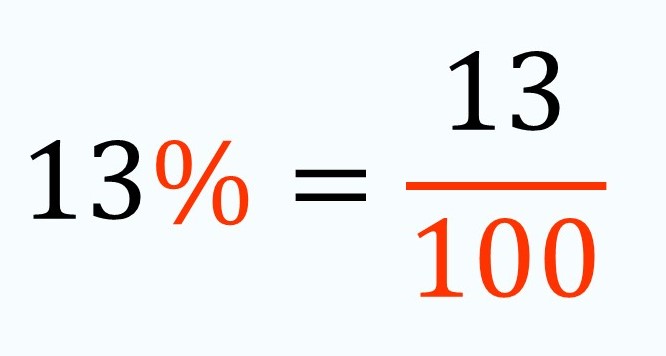
what is the history of percentage?
The concept of percentages can be traced back to ancient civilizations, where early humans used simple fractions to express ratios and proportions. However, the formal development and usage of percentages as we know them today began much later in history.
The origin of the term “percentage” can be attributed to the Latin phrase “per centum,” which means “per hundred.” This term was commonly used during the Middle Ages in Europe. It was a way of expressing fractions with a denominator of 100, making calculations and comparisons more convenient.
The modern concept of percentages gained prominence during the Renaissance and the Age of Enlightenment. Mathematicians and scholars began to refine and formalize mathematical notation, including the use of percentages. The concept became more widely accepted and recognized as an effective way to express proportions and make calculations easier.
One significant historical figure who contributed to the development of percentages was the Italian mathematician Luca Piccioli. In his book “Summa de arithmetical, geometric, proportion et proportionality” published in 1494, Piccioli introduced the concept of “per hundred” and its representation using a symbol similar to the modern percentage sign (%).
Over time the usage of percentages expanded across various fields and became an integral part of everyday life. In the 19th and 20th centuries, with the advancement of mathematics and the spread of education, percentages became even more widespread and commonly used in business, finance, statistics, and other disciplines.
Today, percentages are an essential tool for calculations, comparisons, and data analysis in numerous fields. They provide a standardized and easily understandable way to express proportions, ratios, and changes. The concept of percentages continues to evolve, with new applications and uses emerging in different areas, such as economics, science, and social sciences.
In summary, the history of percentages dates back to ancient times, but the formal development and widespread usage of the concept began during the Middle Ages and gained momentum during the Renaissance. The contributions of mathematicians and scholars, along with the need for a standardized method of expressing proportions, led to the establishment of percentages as a fundamental mathematical concept that is widely used in modern society.

Formula to Calculate Percentage
he formula to calculate a percentage is relatively straightforward and involves three components: the part, the whole, and the constant 100. Here’s the formula:
Percentage = (Part / Whole) × 100
To calculate a percentage, follow these steps:
- Identify the part: Determine the specific value or quantity that you want to find the percentage of. Let’s call this value “Part.”
- Identify the whole: Determine the total value or quantity that the part is related to. Let’s call this value “Whole.”
- Divide the part by the whole: Divide the value of the part by the value of the whole.
- Multiply by 100: Take the quotient obtained in the previous step and multiply it by 100.
The result will be the percentage value of the part in relation to the whole.
For example, let’s say you want to find the percentage of a test score. If you scored 75 out of 100 marks, you can calculate the percentage as follows:
Percentage = (75 / 100) × 100 = 75%
This means that your score of 75 out of 100 corresponds to 75% of the total marks.
Similarly, you can use this formula to calculate percentages in various scenarios, such as finding the percentage increase or decrease, determining proportions, or analyzing data. The formula allows you to express a part in relation to a whole as a standardized percentage value.

Examples of Percentage
Certainly! Here are some examples that illustrate the application of percentages in different scenarios:
- Discounts: Percentages are commonly used to calculate discounts during sales or promotions. For instance, if an item is marked down by 20% and its original price was $50, the discounted price would be $40 (20% of $50 is $10, so subtracting $10 from $50 gives $40).
- Interest Rates: Percentages are used to express interest rates in financial transactions. For example, if you have a savings account with an annual interest rate of 5% and you deposit $1,000, you will earn $50 in interest over the course of one year (5% of $1,000 is $50).
- Population Growth: Percentages are useful for understanding population growth rates. For instance, if a city’s population grows from 10,000 to 12,000 people, the growth rate can be calculated as 20% ([(12,000 – 10,000) / 10,000] × 100).
- Grades: Percentages are often used in education to represent grades. For example, if a student receives a score of 85 out of 100 on a test, their grade would be 85%.
- Market Share: Percentages are used to analyze market share in business. For instance, if a company has $500,000 in sales out of a total market size of $2 million, its market share would be 25% ([$500,000 / $2,000,000] × 100).
- Polling Results: Percentages are frequently used to present polling or survey results. For example, if a survey shows that 60% of respondents prefer Product A, it means that 60 out of 100 respondents selected Product A as their preference.
- Tax Rates: Percentages are used to calculate tax amounts. For instance, if a sales tax rate is 8% and you make a purchase worth $100, the tax amount would be $8 (8% of $100).
These examples demonstrate how percentages are employed in various contexts, including finance, economics, education, statistics, and more. Percentages provide a convenient and standardized way to represent proportions, changes, and comparisons, making them widely applicable in numerous real-life scenarios.